Gio of Beautiful With Brains suggested that I do a post on this after an Instagram conversation about SPF, and how it doesn’t actually tell you how much longer you can stay in the sun without burning. So what exactly does a sunscreen’s SPF mean in terms of sun protection?

I’ve touched on this topic a few times in my other posts on sunscreen like How SPF Changes With How Much Sunscreen You Use and my video on Why DIY Sunscreen Doesn’t Work, but I’ve never tackled it directly before. So here it is!
How sunscreen SPF is tested
SPF testing of sunscreens is performed on actual human volunteers in a laboratory. The sunscreen is applied at 2 mg per cm2 (equivalent to around ¼ teaspoon for the face, or a shotglass full for the entire body). A UV lamp is shone on bare skin and sunscreened skin, and the times required for redness (erythema) to show up are fed into this formula to work out SPF:
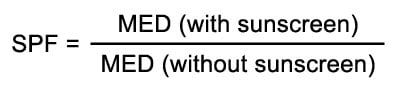
(MED stands for minimum erythemal dose, i.e. how much UV was required for red sunburn to occur.)
For example, if a volunteer normally gets burned in 5 minutes under the lamp, a sunscreen that stops them from burning for 75 minutes (15 times longer) would be classified as SPF 15:
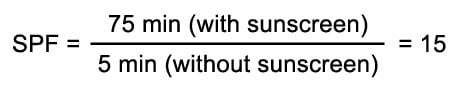
(There’s ongoing research to replace this into an in vitro test that doesn’t require exposing people to cancer-causing UV rays, but right now they’re not reliable enough.)
So SPF means how many times more UV your skin can handle before burning with sunscreen on, compared to nothing at all.
So SPF tells you how much longer you can stay in the sun… doesn’t it?
Well, no. It’s a common misconception that SPF refers to how much longer you can stay in the sun with the sunscreen on before getting sunburnt, but this isn’t accurate. In the laboratory, the UV output from the lamp is consistent, so the UV dosage is proportional to time, and the SPF equation works when we substitute in the times required for burning.
However, in the real world, the UV wavelengths from the sun that cause sunburn (erythemal UV) vary quite a lot throughout the day. The atmosphere absorbs erythemal UV, so if the sun is lower in the sky, less erythemal UV will hit you.
Here’s a graph showing the UV Index, a number directly proportional to the amount of erythemal UV present, over Sydney in summer. The higher the UV index, the more UV there is.
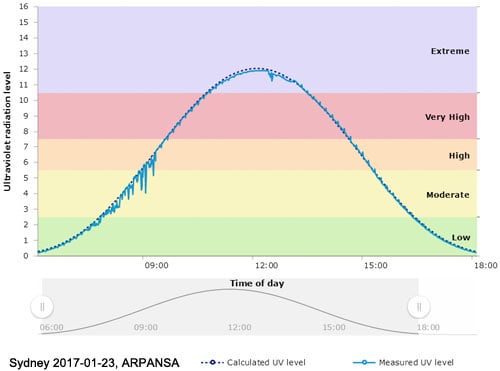
At noon on this particular day in Sydney, the UV level is over 10 times the level at 7 am (UV index of 11.9 vs 0.9). So if you normally get burned after 20 minutes in the sun at 7 am, at midday you’d only last 22.7 minutes at midday even with SPF 15 sunscreen. This is significantly less than the 300 minutes or 5 hours you’d predict with the “how much longer you can stay in the sun” interpretation! Even with SPF 50 sunscreen you’d only last 75 minutes.
In reality, it’s even more complex than this – clouds block out UV as well, and if you’re standing in the wrong place, reflective surfaces like snow and water can double the amount of UV you receive.
Will high SPF sunscreen be enough?
SPF is one of the most important things to look for in a sunscreen, but it isn’t everything.
Here’s a graph showing the UV wavelengths that cause sunburn (in the red line, with the actual output of UV from the sun in blue. Note that this is a log scale, so the graph should actually be far steeper on the left than it appears):
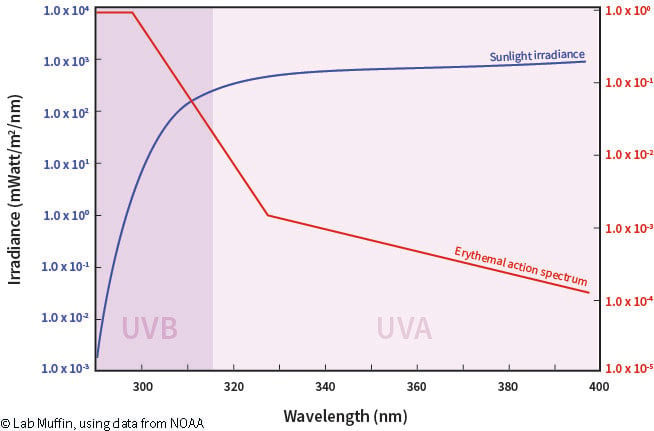
Note that the UV wavelengths that cause sunburn are mostly shorter wavelengths of UV, termed UVB. For UV, shorter wavelengths are more energetic but penetrate the skin less deeply. However, longer wavelength UVA is also harmful (read all about that here: Why you should protect yourself from UVA), and SPF doesn’t really take this into account. To ensure protection against UVA, look for either a PPD rating on your sunscreen or the words “broad spectrum”. In some countries like Australia, sunscreens with certain SPFs have to be broad spectrum, but in the US that isn’t the case.





Do windows block out UV as well? I’m really lazy when it comes to applying sunscreen indoors…
They block out UVB but not UVA, though it shouldn’t be too much of a problem if you’re not in direct light 🙂
Thanks for this explanation! The time-based theory has never fully made sense to me – it should follow that if you usually burn in 10 minutes and apply SPF 60 you’d have 10 hours of sun protection, which doesn’t jibe with the recommendation to reapply every few hours (though I guess a lot of that has to do with it wearing off as well). This makes a lot more sense.
Good point! Not reapplying is a big issue.
I love this post so much, Michelle, especially the section that illustrates how lab conditions and real-life conditions are wildly different.
This is such a complex subject, but I often think that there’s a fairly simple way to improve consumer sunscreen use: cut the test amounts in half (as per realistic use) and adjust the SPF labelling accordingly. However, when I suggested that to a big-brand chemist, he felt that re-educating the public would be too great a challenge. I don’t agree, especially given that the SPF rating itself was a marketing strategy in the first place.
Then again, educating about UVA ratings isn’t easy either. #thestruggleisreal
I thought that was the obvious solution too, but apparently 2 mg/cm2 is required for reproducible results! I can’t remember which ref it was that said that but it should be one of the three down the bottom here: https://labmuffin.com/spf-changes-how-much-sunscreen-use/ From memory it was to do with the microscopic bumpiness of skin.
Rats. How disappointing that there’s a logistical reason for the amount used in lab tests. (And how odd that the R&D guy I spoke with didn’t mention it.) Thanks so much for that!
This was such a useful explanation – I’d never quite understood how it worked.
Hurray! Mission accomplished 🙂
In a Choice survey of Australian sunscreens a while back they mentioned that the human factor of testing can produce varied results. They also said that in one US survey the lab results varied according to what the lab was told the SPF was beforehand. Measuring SPF doesn’t sound like a very exact science right now. Makes me wonder how many products are what they say on the tin. 🙁
https://www.choice.com.au/spf#testing
I worry about that too! But it’s certainly better than using nothing, or untested products. I think sometimes aggregated reviews are underrated in this regard – for example, there are some sunscreens which have lots of reviews on Amazon and Makeupalley saying that people got burned while wearing them, which would make me avoid that sunscreen regardless of the label…
Ah thanks for this post! It’s always interesting to learn how products are actually tested in the lab (what assumptions they use and how these differ from the real world). My takeaway from this is that reapplying is non-negotiable, no matter how high your spf. :))
Sorry if this is a dense question, but do we reapply because the UV blocking capacity of the sunscreen has worn off/out? I’m not talking about it washing off or wearing off, but that you’ve been exposed to x amount of UVA/B that the sunscreen can handle, and now it’s time to put a fresh batch on?
Partly yes, but it really depends on the sunscreen – if it’s not photostable that will be the reason, but most modern sunscreens are pretty photostable.
What do you think of laying sunscreens? I use an spf moisturizer and then an actual sunscreen. Am I reducing the efficacy or improving it by applying more sunscreen overall?
You should be improving it… unless there are ingredients that inactivate each other.
Hi, thank you for your blog, very informative! I have a question about protection from the sun. A lot of sites (e.g. beautipedia), emphasize the importance of applying sunblocks all year around. However, the UV index in my city almost never rises above 1 from mid October till April and even World Health Organization writes that no protection is needed. I am confused – am I OK without sunblocks during these months? Why should I protect mtsrlf from something that is just not there-it gets dark at 3 p m!
You’re right, it depends on where you are! There’s more info on this post on vitamin D and sunscreen about the guidelines based on UV index 🙂
Hi!
Thanks for the informative post. I came on your site to read one review and haven’t left yet!
My question is: how effective are normal clothes in terms of UVA and UVB protecton? I often wear long sleeves and pants instead of the slip, slop and slap.
Thanos!
good post and clear explanation. We throw around the term SPF a lot but a lot of people don’t really know what it means or the science behind it.
A nice and clearcut view on SPF which i didn’t know earlier but by reading your post i actually know what sunscreen i need to buy
Help me understand…
If a sunscreen says to reapply every 4 hours , and I was in a dark room from the application time till 4 hours later, would it still need to be reapplied even with no exposure to sun?
Great and good post and clear explanation. We throw around the term SPF a lot but a lot of people don’t really know what it means or the science behind it.
very informative post.A nice and clearcut view on SPF which i didn’t know earlier but by reading your post i actually know what sunscreen i need to buy
I found this blog very informative and helpful. It helped me clear my all doubt about SPF. It made me learn many aspect of sunscreen and the clear understanding of what you need.
I was searching for SPF for ages! My skin was tanning while playing pickleball.